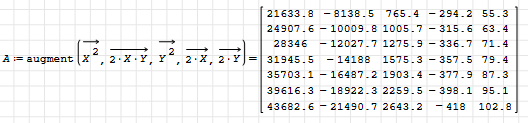The work with not quadrat matrix.
How better solve?
See please the attached sm-file.
1-Asteroid-5-Points.sm (25 KiB) downloaded 125 time(s).

Wrote

The work with not quadrat matrix.
How better solve?

As it looks, the blue planet and green voyager are tangent.
Take care Valery ... Jean.

1-Asteroid-5-Points.sm (34 KiB) downloaded 116 time(s).

Hi Valery. You can use dn_LinAlgLLS_SVD or dn_LinAlgLLS_COF or dn_LinAlgLLS_QRorLQ for non-square matrices, instead dn_LinAlgSolve.

1-Asteroid-5-Points.sm (27 KiB) downloaded 109 time(s).

Best regards.
Alvaro.

Thanks Alvaro.
10-2-Asteroid-7-points.sm (21 KiB) downloaded 125 time(s).

A little more compact.



Best regards.
Alvaro.

Thanks Alvaro.
New problem with Ranks
10-2-Asteroid-7-points-Rank.sm (16 KiB) downloaded 114 time(s).

Wrote

... New problem with Ranks

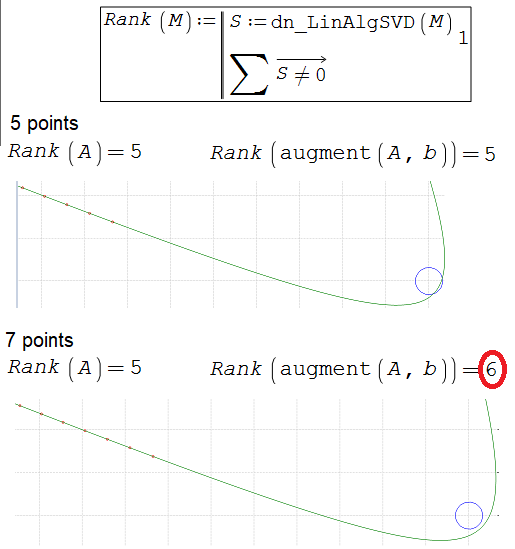
Hi Valery. SMath really needs to improve on linear algebra. As a workaround, you can redefine rank with a plugin



Also, the problem with rank is not that it can't deal with complicated arrays, it can't handle simple ones either



10-2-Asteroid-7-points-Rank.sm (19 KiB) downloaded 115 time(s).

Best regards-
Alvaro.

Why?
10-2-Asteroid-7-points-Rank.sm (28 KiB) downloaded 121 time(s).

Wrote

Why?

Hi. Due to numerical errors. These ranks are evaluated with numerical procedures. That means that for some cases they must necessarily fail. You can introduce some kind of tolerance in the function. Maple also fails in this example.



This shows that the rank function that is executed is that of maple.



However, I don't know how to call Maxima's rank function, it is not in the Takeover options.

Here some notes about how to handle a little better the issue.

10-2-Asteroid-7-points-Rank.sm (35 KiB) downloaded 113 time(s).

Best regards.
Alvaro.

Maxima gives the correct answer. Yet I think that maple is not to blame, because maple(rank(M)) sends 4 to maple. At least this happens with Maxima(rank(M)).

In Maxima I have a workaround for such cases. First I convey the definition of M to Maxima and then call rank(M). The format "$...§" conveys everything inside the markup as verbatim expression to Maxima. without giving SMath the chance to interfere.

Should not be too complicated to add rank() to the takeover candidates.


10-2-Asteroid-7-points-Rank _Kr.sm (40 KiB) downloaded 119 time(s).

Hi Martin.

Wrote

Maxima gives the correct answer ...

Nope. The issue is about a matrix C=augment( A,b ), where b is a column vector so, it must to have the same rank as A.

Wrote

... Yet I think that maple is not to blame, because maple(rank(M)) sends 4 to maple. At least this happens with Maxima(rank(M)).

Either. In some way maple holds the rank function and evaluates it on its own kernel. Actually, the example with the matrix M is for show that.

Best regards.
Alvaro.