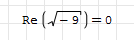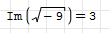Is there a way to get ride of complex numbers? - Messages
#1 Posted: 5/26/2021 1:18:59 AM
hi Folks, I am programming some equations and there is a requirement for a summation of terms, each term being a square root of a function of several variables. The method requires ignoring any negative results, i.e. where the square root of a negative number will lead to a complex number.
The terms are all have identical variables and it would be ideal if I can perform some operation on the general case term, so that the imaginary results just vanish.
The terms are all have identical variables and it would be ideal if I can perform some operation on the general case term, so that the imaginary results just vanish.
#2 Posted: 5/26/2021 2:31:38 AM
Hi. You can try to redefine i:=0 and see if get the desired behavior.
Best regards.
Alvaro.
Best regards.
Alvaro.
#3 Posted: 5/26/2021 2:57:00 AM
There is a function called Re that returns the real part of a complex number. See example below
For reference: The counterpart is the function Im, see below.
For reference: The counterpart is the function Im, see below.
#4 Posted: 5/26/2021 10:11:26 AM
#5 Posted: 5/26/2021 7:01:12 PM
hi folks, thanks for your contributions
the way I've solved my dilemma was to multiply each term by (X>0) so that whenever X is less than zero the sqrt(X*(X>0)) becomes zero.
the way I've solved my dilemma was to multiply each term by (X>0) so that whenever X is less than zero the sqrt(X*(X>0)) becomes zero.
#6 Posted: 5/26/2021 8:09:39 PM
the way I've solved my dilemma
You have solved nothing yet from nothing to pass QA !
#7 Posted: 5/26/2021 10:02:06 PM
Your description is too general w/o the formula.
#8 Posted: 5/27/2021 12:25:47 AM
Hi Jim. Actually your dilemma isn't trivial and the solution that you found it's complete in the sense that you extend over the integers an operation only well defined for the natural numbers. For integers, rationals, reals, complexes, vectors, matrices, tensors ... are only conventions based on definitions by convenience, very very good ones ... but not theorems.
For example Maple have the function surd for deal with roots with integers when the usual convention doesn't work. Because power don't commute have two inverses, one by the left and other by the right, roots and logarithms, complicating the things. This is the help for the surd function from Maple website:
https://www.maplesoft.com/support/help/Maple/view.aspx?path=surd
As you can see, if you ask to Maple for convert surd, it returns just x^(1/n).
So, you can define your own function pow3(x) = x^3 * (x > 0). Or maybe more general some CheckPos(x) for make more readable your expression.
Best regards.
Alvaro.
For example Maple have the function surd for deal with roots with integers when the usual convention doesn't work. Because power don't commute have two inverses, one by the left and other by the right, roots and logarithms, complicating the things. This is the help for the surd function from Maple website:
https://www.maplesoft.com/support/help/Maple/view.aspx?path=surd
As you can see, if you ask to Maple for convert surd, it returns just x^(1/n).
So, you can define your own function pow3(x) = x^3 * (x > 0). Or maybe more general some CheckPos(x) for make more readable your expression.
Best regards.
Alvaro.
#9 Posted: 5/27/2021 7:47:21 AM
Your description is too general w/o the formula.
Attach the *.sm document.
#10 Posted: 5/27/2021 9:25:19 AM
Attach the *.sm document.
... do some effort:
split that monster, zap subscript, make minimalist like visiting doctor.
Page10 Split Monster.sm
-
New Posts
-
No New Posts